| ⋄ Friedrich Engels schrieb die Kapital-Bände 2 und 3 bekanntlich auf Grundlage von Manuskripten, die Marx hinterlassen hat. Die neue Marx-Engels-Gesamtausgabe macht diese erstmals zugänglich. ⋄ Insbesondere im Ausland ist die für viele Marxist*innen eine erstmalige Gelegenheit, Einblick in das „Rohmaterial“ des Kapitals zu bekommen, was die Debatte aktuell stark anregt. ⋄ Kenji Mori bespricht ein Manuskript über die Wirkung der Umschlagszeit auf das fixe und zirkulierende Kapital, das im dritten Band nur mit einem Verweis auf den zweiten abgehandelt wird. ⋄ In diesem unterscheidet Marx die Wirkung der Umschlagszeit auf eine Profitrate auf den Kostpreis und eine auf das vorgeschossene Kapital. ⋄ Mit Hilfe einer Input-Output-Simulation überprüfte Mori die Plausibilität der Marxschen Manuskripte und betrachtete die Durchschnittsprofitrate mit. |

Es ist im wahrsten Sinne des Wortes ein MEGA-Projekt. Die zweite und grunderneuerte Marx-Engels-Gesamtausgabe hat sich zum Ziel gesetzt, wirklich den vollständigen schriftlichen Nachlass von Karl Marx und Friedrich Engels zu edieren und der Öffentlichkeit zugänglich zu machen. Sollte sie tatsächlich 2025 abgeschlossen werden, lägen 100 Jahre Entstehungsgeschichte seit Beginn der ersten MEGA-Edition hinter den 114 dicken Bänden. Aber das Projekt war keineswegs nur ein Spielplatz für Marxologen und Handschriftenexperten. Insbesondere in den USA hat die Veröffentlichung der Manuskripte und Vorarbeiten zu den Kapital-Bänden viele Diskussionen neu angestoßen. Oftmals ist erst seit wenigen Jahren nachzuverfolgen, was Marx für sich selbst schrieb, auf welchen Manuskripten die Veröffentlichung der Bände 2 und 3 durch Engels beruhte und wie er sie verändert hat. Dabei füllen sich auch einige Leerstellen. Die zweiteilige Artikelserie soll nun zwei Studien zu den besagten Manuskripten vorstellen. Beide beschäftigen sich insbesondere mit der Bildung der Profitrate.
Die Umlaufgeschwindigkeit und die beiden Profitraten
Zunächst soll es um einen Aufsatz von Kenji Mori zur Frage des Einflusses der Umschlagszeit auf die Verwertung des fixen und zirkulierenden Kapitals gehen. Das Problem, um das es zunächst geht, wurde hier schon mehrmals angesprochen (siehe hier & hier). Während in der Regel immer die jährliche Profitrate betrachtet wird, besitzt jedes Kapital je nach Beschaffenheit der Branche eine andere Umschlagszeit, d.h. die Zeit, in der das Kapital, das zu Beginn in den Produktionsprozess gesteckt wurde, sich verwertet hat. Das bedeutet, dass neben der Mehrwertrate und der organischen Zusammensetzung auch die Umschlagszeit eine Rolle bei der Bildung der Profitrate spielt oder man, besser gesagt, zwischen einer realen und einer jährlichen Profitrate unterscheiden müsste. Strittig ist hierbei insbesondere der Punkt, wie sich der Wert des konstanten Kapitals bei einer Verringerung der Umschlagszeit verhält. Das konstante Kapital teilt sich ja bekanntermaßen in das zirkulierende Kapital auf, das während der Produktion vollständig verbraucht wird (z.B. Weizen bei der Produktion von Brot) und in das fixe Kapital (z.B. der Ofen und die Bäckerei), das pro Umschlag nur einen Teil ihres Werts an das Produkt übertragen.
Kenji Mori analysierte zwei Manuskripte aus den Jahren 1967/68, die in Band 4.3 der zweiten Abteilung veröffentlicht sind. Hier beschäftigt sich Marx tiefergehend mit dem Zusammenhang zwischen Umschlagszeit, Mehrwertrate und Profitrate. Die Inhalte der Manuskripte drücken Moris Meinung nach etwas völlig anderes aus, als Engels im dritten Band des Kapitals schrieb. Engels kürzte im auf diesen Manuskripten beruhenden Teil des Kapital stark ein und verwies darauf, dass der Zusammenhang zwischen Umschlagszeit und variablem Kapital bereits in Band 2 erläutert worden sei; aber eben nicht der Zusammenhang zum konstanten. Das führte zu zweierlei Missverständnissen. Entweder wurde die Wirkung der Umschlagszeit auf das konstante Kapital in der Folge ignoriert oder es wurde Marx fälschlicherweise vorgeworfen, sie ignoriert zu haben.
In seinem Manuskript nun unterscheidet Marx zwei Profitraten: eine auf das vorgeschossene Kapital und eine auf den Kostpreis (näheres hier). Die erste bezeichnet er mit R, die andere mit Pi. Daneben spielen noch das vorgeschossene Kapital C, der Kostpreis K, die Mehrwertrate M und die Umschlagszahl pro Jahr U eine Rolle. Die beiden Profitraten unterscheiden sich durch die Identität:
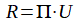
Die jährliche Profitrate ist also Produkt der Umschlagszahl und der Profitrate pro Umschlag. Es ist leicht einzusehen, dass daher folgende Bestimmungen gelten:
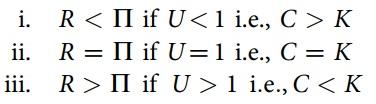
Man könnte hier die Umschlagszahl auch als Maß für die technische Zusammensetzung betrachten, also einen Parameter, der nicht nur Auskunft über die Zusammensetzung des Kapitals gibt, sondern auch über eine Veränderung des Produktionsprozesses selbst.
Marx rechnete in betreffendem Manuskript nun ähnlich, wie bei seiner Transformationstabelle ein Beispiel numerisch durch. Die Mehrwertrate sollte 100% betragen, die organische Zusammensetzung 4 und das Verhältnis von fixem zu zirkulierendem Kapital ebenfalls 4. Mit diesen Werten rechnet Marx zunächst für das zirkulierende Kapital vor:
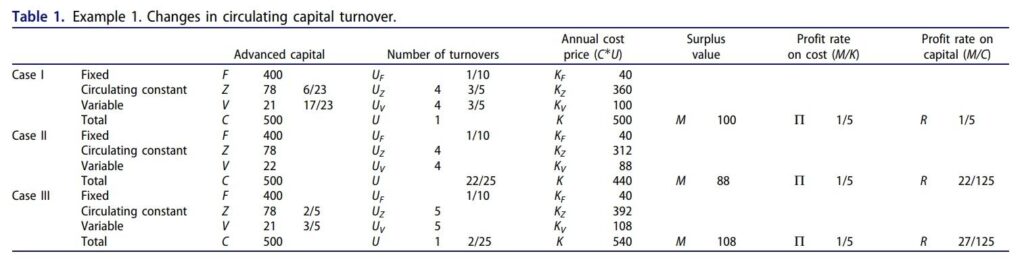
Das Ergebnis ist recht interessant. Die Veränderung der Umschlagszeit muss natürlich die Zusammensetzung des vorgeschossenen Kapitals unberührt lassen, da dieses ja bereits verausgabt war. Da die realisierte Profitrate (ohne, dass die Durchschnittsprofitrate hier bereits eine Rolle spielt) auf den jeweiligen Kostpreis aufgeschlagen wird (im Übrigen eine Feststellung, die in der marxistischen Debatte nicht unumstritten ist), ändert sich die Profitrate auf das vorgeschossene Kapital insgesamt und zwar genau so, dass sich die Umschlagszahl und das Verhältnis von R zu Pi kompensieren.
Eine ähnliche Tabelle hat Marx in dem Manuskript zwar nicht für das fixe Kapital aufgestellt, sie lässt sich aber leicht an Hand der wörtlichen Beschreibung des Mechanismus leicht rekonstruieren.

Das Beispiel leuchtet ein. Nutzt sich eine Fabrik oder Maschine schneller ab als gedacht, sinkt natürlich der Profit auf den Kostpreis, während die Mehrwertrate, die den Neuwert auf das vorgeschossene Kapital aufschlägt konstant bleiben muss. Hält die Maschine länger, muss nicht so schnell eine nachgekauft werden und der Profit auf den Kostpreis – in welchem der Unterschied zwischen variablem und konstantem Kapital ausgelöscht ist – steigt.
Kurz gesagt erhöht die Umschlagszeit allgemein die Profitrate. Eine schnellere Vernutzung des zirkulierenden Kapitals erhöht die Profitrate auf das vorgeschossene Kapital, während eine schnellere Vernutzung des fixen Kapitals die Profitrate auf den Kostpreis senkt.

Dies ist in sofern eine wichtige Ergänzung zum dritten Kapitalband, als dass Engels nur den Umschlag des zirkulierenden Kapitals betrachte hatte und das auch nur durch einen Verweis.
Aber stimmt das?
Nun stellt sich natürlich nicht nur die Frage, was Marx für eine Auffassung in den Manuskripten vertreten hat, sondern man muss auch diskutieren, wie plausibel diese Modellannahme ist. Um dies herauszufinden, hat Mori ein geschlossenes Direktes Leontieff Modell (DLM) entworfen, um Marxens Gedanken nachzuvollziehen, also einen Input-Output-Algorithmus (Näheres hier). Dieses unterscheidet sich jedoch in zweierlei Hinsicht vom Inhalt der Manuskripte. Erstens rechnet es alles in Preisen und abstrahiert damit von der Arbeitswertlehre und dem damit verbundenen Transformationsproblem. Gerechtfertigt wird dies durch die Tatsache, dass zumindest in diesem Modell keine Umrechnung von Werten in Preise überhaupt notwendig ist, sondern ohnehin nur Preise verglichen werden. Die hier diskutierte zweifache Profitrate ist etwas anderes als die Diskussion, ob es eine Arbeitswertprofitrate und eine monetäre Profitrate gibt. Zweitens wurde die Bildung der Durchschnittsprofitrate mit ins Kalkül gezogen und die Preise so berechnet, dass sie nach jeder Periode den Markt räumen. Diese beiden Restriktionen sind wahrscheinlich schon eher in der marxistischen Debatte umstritten und charakteristisch für den genutzten Ansatz über Input-Output-Rechnung. Zusätzlich nahm Marx noch eine konstante Abnahme des Werts des fixen Kapitals und die Vernachlässigbarkeit der Entwertung auf die Produktivität an. Theoretisch ließe sich das in einer Input-Output-Simulation auch realistischer gestalten. Es wurde aber bewusst auf die Betrachtung dieses zusätzlichen Einflusses verzichtet bzw. für eine Nachbetrachtung aufgehoben.
Die Erkenntnisse waren dreierlei Natur. Erstens sorgt die Verringerung der Umschlagszeit sowohl beim fixen als auch beim zirkulierenden Kapital für eine Erhöhung der individuellen Profitrate. Beim fixen Kapital ist das klar. Wenn eine Maschine länger hält, verringert sich ihr jährlicher Kostpreis. Beim zirkulierenden Kapital ist es nicht ganz so einfach. Denn je häufiger das Kapital jährlich umschlägt, desto mehr zirkulierendes Kapital muss auch gekauft werden. Es zeigt sich aber, dass die einhergehende Erhöhung der Mehrwertrate diesen Effekt nicht nur kompensiert, sondern überkompensiert. Die Durchschnittsprofite wird allerdings unterschiedlich beeinflusst. Während die Erhöhung der Mehrwertrate diese im Allgemeinen steigert, senkt die schnellere Vernutzung des gesamten fixen Kapitals diese wieder. Die Wirkung der Umschlagszeit hängt also stark von der genauen Zusammensetzung des individuellen und gesellschaftlichen Kapitals ab, sowie dem Verhältnis der verschiedenen Umschlagszeiten auf fixes und zirkulierendes Kapital. Vielleicht hat daher Engels davon abgesehen, die Wirkung der Umschlagszeit auf die einzelnen Bestandteile des konstanten Kapitals so genau nachzuverfolgen, wie Marx dies in seinen Manuskripten tat. Dennoch eröffnet der Nachvollzug dieses Manuskripts spannende Einsichten in den Marxschen Forschungs- und Engelsschen Darstellungsprozess. Am Freitag erscheint der zweite Teil zu den Manuskripten.
Literatur:
Mori, K. (2024): Dual rates of profit and the turnover of capital in Karl Marx’s post-Capital manuscripts in 1868. An interpretation in terms of input-output analysis. In: The European Journal of the History of Economic Thought. Online First. DOI: 10.1080/09672567.2024.2384881.

Ein Kommentar